Avviso importante: quanto segue non vuole essere la riflessione di un matematico, ma quella di una persona che ha passione per la politica e che ha interesse a comprendere a 360 gradi il modo in cui viene trattato il suo voto.
Problema che si vuole affrontare
Si vuole eleggere un organo collegiale, cioè un organo che è costituito da un certo numero di componenti. Sappiamo che:
- questo organo avrà
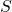 componenti;
componenti; - è prevista la presentazione di liste concorrenti, ciascuna contenente un numero di candidatura pari ad almeno
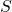
Supponiamo che si siano presentate tre liste, e che i voti ottenuti da queste siano i seguenti:
| Nome liste | Voti ottenuti |
|---|---|
| Lista concorrente n.1 | 5088 (53.72%) |
| Lista concorrente n.2 | 2943 (31.07%) |
| Lista concorrente n.3 | 1440 (15.20%) |
| TOTALE | 9471 (100%) |
Supponiamo che ![]() : come facciamo a convertire i 9471 voti totali in 24 seggi? Le spiegazioni seguenti si rifanno al PDF Meccanismi elettorali: la matematica è un opinione del prof. Paolo Acquistapace (pdf che mi rimane nel cuore, suggeritomi da un docente delle superiori nell’ormai lontano 2018 per approcciarmi all’argomento). Si fa riferimento anche alle pagine Wikipedia Sistemi proporzionali e Metodo Hare-Niemeyer.
: come facciamo a convertire i 9471 voti totali in 24 seggi? Le spiegazioni seguenti si rifanno al PDF Meccanismi elettorali: la matematica è un opinione del prof. Paolo Acquistapace (pdf che mi rimane nel cuore, suggeritomi da un docente delle superiori nell’ormai lontano 2018 per approcciarmi all’argomento). Si fa riferimento anche alle pagine Wikipedia Sistemi proporzionali e Metodo Hare-Niemeyer.
Premessa: maggioritario VS proporzionale
In generale nei sistemi elettorali si fa distinzione tra due tipologie di metodi:
- metodi proporzionali,
che permettono una distribuzione dei seggi proporzionale al numero di voti ottenuti dalle liste; - metodi maggioritari,
che favoriscono nella distribuzione dei seggi coloro che hanno ottenuto il maggior numero di voti, a discapito di coloro che hanno ottenuto meno voti (quindi una lista che ha ottenuto, ad esempio, il dei voti, potrebbe ottenere una percentuale di seggi
dei voti, potrebbe ottenere una percentuale di seggi 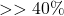 ).
).
Si tenga a mente che non è facile definire in modo oggettivo un sistema elettorale come proporzionale o maggioritario: molto spesso si introducono correttivi (come soglie di sbarramento1, premio di maggioranza2) o addirittura si adottano forme ibride (come per le elezioni del Parlamento Italiano3, in entrambe le camere abbiamo c.a 60% dei seggi eletti con metodo proporzionale e c.a. 40% dei seggi eletti con maggioritario).
E’ comunque possibile individuare in letteratura alcuni metodi propriamente maggioritari e altri propriamente proporzionali. Quello che noi faremo in questo post è affrontare uno dei principali metodi propriamente proporzionali: il metodo Hare-Niemeyer (generalmente noto come metodo Hare, o metodo dei quozienti e più alti resti).
1 Soglia di sbarramento significa introdurre una percentuale minima di voti che una lista deve ottenere per avere diritto a seggi in un organo. Le liste che non ottengono quella percentuale vengono escluse dalla distribuzione di seggi prima dell’applicazione dell’algoritmo. Celebre è la soglia di sbarramento al 10% per le elezioni della Grande Assemblea Nazionale turca (parlamento unicamerale della Turchia), che limita fortemente l’accesso dei partiti alla distribuzione dei seggi: nelle elezioni parlamentari del 2002 solo due partiti entrarono in parlamento, mentre cinque partiti con percentuali di voto comprese tra il 5% e il 10% dei voti rimasero fuori dal parlamento.
2 Il premio di maggioranza è una feature introdotta in alcuni sistemi di voto proporzionale che mira a bilanciare governabilità (si vuole agevolare la lista vincitrice) e rappresentabilità (il principio su cui si basano i sistemi proporzionali). E’ una distorsione dell’idea alla base del sistema proporzionale perchè la lista vincitrice ottiene un numero di seggi maggiore rispetto a quelli che otterrebbe con un sistema propriamente proporzionale. Esempio di premio di maggioranza si ha nel Porcellum (legge elettorale italiana dal 2005 al 2016), che prevedeva l’assegnazione in ogni caso di almeno 340 seggi (su 630) della Camera dei Deputati alla coalizione più votata.
3 Cosiddetto Rosatellum. Per maggiori informazioni: https://it.wikipedia.org/wiki/Legge_Rosato
Metodo Hare-Niemeyer: quozienti interi e più alti resti
Il metodo è stato ideato dal politico britannico Thomas Hare. Si considera la seguente proporzione
![]()
dove ![]() è il numero di voti totali ed
è il numero di voti totali ed ![]() è il numero di seggi da assegnare. Ricordandoci come si calcola il termine ignoto di una proporzione (per chi avesse un vuoto rimando al seguente post di skuola.net: clicca qui) otteniamo
è il numero di seggi da assegnare. Ricordandoci come si calcola il termine ignoto di una proporzione (per chi avesse un vuoto rimando al seguente post di skuola.net: clicca qui) otteniamo
![]()
Poniamo il metodo nel modo che segue
- Variabili utilizzate
Le variabili utilizzate sono le seguenti:- Variabili da inizializzare all’avvio
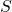 consiste nel numero di seggi da distribuire (inizializzare col valore desiderato);
consiste nel numero di seggi da distribuire (inizializzare col valore desiderato);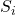 consiste nel numero di seggi assegnati alla lista
consiste nel numero di seggi assegnati alla lista 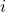 -esima (inizialmente
-esima (inizialmente 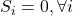 );
);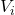 consiste nel numero di voti ottenuti dalla lista
consiste nel numero di voti ottenuti dalla lista 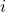 -esima (inizializzare con i voti ottenuti);
-esima (inizializzare con i voti ottenuti);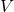 consiste nei voti totali (si ponga
consiste nei voti totali (si ponga 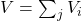 ).
).
- Variabili che utilizzeremo più avanti
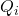 consiste nel quoziente relativo alla lista
consiste nel quoziente relativo alla lista 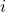 -esima
-esima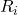 consiste nel resto relativo alla lista
consiste nel resto relativo alla lista 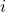 -esima, ottenuto da
-esima, ottenuto da 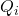
- Variabili da inizializzare all’avvio
- Calcolo dei quozienti
Per ogni lista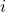 -esima che ha ottenuto
-esima che ha ottenuto 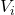 si calcola il quoziente
si calcola il quoziente 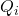
![Rendered by QuickLaTeX.com \[Q_i=\frac{S}{V} \cdot V_i\]](https://www.ifrax.it/wp-content/ql-cache/quicklatex.com-58c149af2eff8d7014fb55f0f00b9567_l3.png)
- Prime assegnazioni di seggi
Per ogni quoziente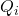 calcolo la parte intera
calcolo la parte intera ![Rendered by QuickLaTeX.com [ Q_i ]](https://www.ifrax.it/wp-content/ql-cache/quicklatex.com-cc903944263456630a2b618601ba5541_l3.png) e assegno alla lista
e assegno alla lista 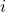 -esima
-esima ![Rendered by QuickLaTeX.com [ Q_i ]](https://www.ifrax.it/wp-content/ql-cache/quicklatex.com-cc903944263456630a2b618601ba5541_l3.png) seggi
seggi ![Rendered by QuickLaTeX.com \[S_i =S_i+ [Q_i]\]](https://www.ifrax.it/wp-content/ql-cache/quicklatex.com-bffce5e2330e1716c85d1cd2f3ccae6a_l3.png)
- Abbiamo finito?
A questo punto abbiamo due possibilità: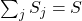 , tutti i seggi sono stati assegnati e l’algoritmo si ferma;
, tutti i seggi sono stati assegnati e l’algoritmo si ferma;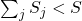 , non sono stati assegnati tutti i seggi, proseguo col passo successivo.
, non sono stati assegnati tutti i seggi, proseguo col passo successivo.
- Calcolo dei resti
Per ogni lista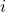 -esima calcolo il resto
-esima calcolo il resto 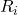 , a partire dal quoziente
, a partire dal quoziente 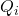 (già calcolato al passo (2))
(già calcolato al passo (2))![Rendered by QuickLaTeX.com \[R_i=Q_i-[Q_i]\]](https://www.ifrax.it/wp-content/ql-cache/quicklatex.com-5185d98dacfcade3ffeede33a96b040c_l3.png)
- Costruzione di una graduatoria
Costruisco una graduatoria con i resti calcolati al punto (5), ordinando dal più grande al più piccolo. Di questa graduatoria considero i primi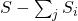 quozienti.
quozienti. - Assegnazione dei seggi rimanenti
Per ogni resto del punto (6) si verifica la lista che lo ha generato, e si assegna un seggio ad essa.
Caso limite (abbastanza remoto): nel caso in cui un resto sia generato da più liste si da la precedenza alle liste che hanno ottenuto più voti.![Rendered by QuickLaTeX.com \[S_i=S_i+1\]](https://www.ifrax.it/wp-content/ql-cache/quicklatex.com-832aad41669945d091b17d1cd975825d_l3.png)
Applicazione del metodo Hare-Niemeyer all’esempio
Riprendiamo l’esempio iniziale e calcoliamo la distribuzione dei seggi
| Nome liste | Voti ottenuti |
|---|---|
| Lista concorrente n.1 | 5088 (53.72%) |
| Lista concorrente n.2 | 2943 (31.07%) |
| Lista concorrente n.3 | 1440 (15.20%) |
| TOTALE | 9471 (100%) |
- Variabili utilizzate
Le variabili utilizzate sono le seguenti:- Variabili da inizializzare all’avvio
- Seggi da distribuire:
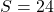
- Variabili dove indicheremo i seggi assegnati alle liste:
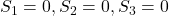
- Voti ottenuti dalle liste:
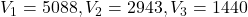
- Voti totali:
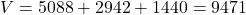
- Seggi da distribuire:
- Variabili da inizializzare all’avvio
- Calcolo dei quozienti
Per ogni lista -esima che ha ottenuto
-esima che ha ottenuto 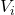 si calcola il quoziente
si calcola il quoziente 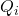 (le prime cinque cifre più significative)
(le prime cinque cifre più significative)
- Prime assegnazioni di seggi
Per ogni quoziente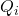 calcolo la parte intera
calcolo la parte intera ![Rendered by QuickLaTeX.com [ Q_i ]](https://www.ifrax.it/wp-content/ql-cache/quicklatex.com-cc903944263456630a2b618601ba5541_l3.png) e assegno alla lista
e assegno alla lista 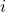 -esima
-esima ![Rendered by QuickLaTeX.com [ Q_i ]](https://www.ifrax.it/wp-content/ql-cache/quicklatex.com-cc903944263456630a2b618601ba5541_l3.png) seggi
seggi
- Abbiamo finito?
Sono stati assegnati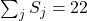 seggi, rimangono da assegnare
seggi, rimangono da assegnare 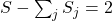 seggi.
seggi. - Calcolo dei resti
Per ogni lista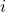 -esima calcolo il resto
-esima calcolo il resto 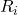 , a partire dal quoziente
, a partire dal quoziente 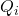 (già calcolato al passo (2))
(già calcolato al passo (2))
- Costruzione di una graduatoria
Costruisco una graduatoria con i resti calcolati al punto (5), ordinando dal più grande al più piccolo. Di questa graduatoria considero i primi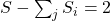 quozienti.
quozienti.
- Primo posto della graduatoria:
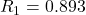 , generato dalla lista n.1
, generato dalla lista n.1 - Secondo posto della graduatoria:
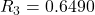 , generato dalla lista n.3
, generato dalla lista n.3 - Terzo posto della graduatoria: scartato, mi interessano solo i primi due quozienti.
- Primo posto della graduatoria:
- Assegnazione dei seggi rimanenti
Per ogni resto del punto (6) si verifica la lista che lo ha generato, e si assegna un seggio ad essa.- Seggio assegnato alla lista n.1 (12 + 1 = 13)
- Seggio assegnato alla lista n.3 (3+1 = 4)
Abbiamo finito!
| Nome liste | Voti ottenuti | Seggi assegnati |
|---|---|---|
| Lista concorrente n.1 | 5088 (53.72%) | 13 |
| Lista concorrente n.2 | 2943 (31.07%) | 7 |
| Lista concorrente n.3 | 1440 (15.20%) | 4 |
| TOTALE | 9471 (100%) | 24 (100%) |
Tabelle riepilogative dei valori calcolati
| Nome liste | Voti ottenuti | (first value) | (final value) | |||
|---|---|---|---|---|---|---|
| Lista n.1 | ||||||
| Lista n.2 | ||||||
| Lista n.3 | ||||||
| Lista generatrice | Assegnazione seggi | |
|---|---|---|
| Lista n.1 | Seggio assegnato alla lista n.1 (12+1=13) | |
| Lista n.3 | Seggio assegnato alla lista n.3 (3+1=4) | |
| Lista n.2 | Scartato |